Permutasi adalah konsep matematika yang berkaitan dengan cara menyusun atau mengatur objek dalam suatu urutan tertentu.
Dalam kehidupan sehari-hari, kita sering menemui situasi yang melibatkan permutasi, seperti menyusun jadwal, menentukan urutan pemenang dalam perlombaan, atau bahkan mengatur tempat duduk di sebuah acara.
Memahami konsep ini tidak hanya berguna dalam pelajaran matematika, tetapi juga dalam logika dan pemecahan masalah.
Melalui artikel ini, kita akan membahas beberapa contoh soal permutasi yang akan membantu kamu memahami cara kerja permutasi dengan lebih mudah dan aplikatif. Yuk, simak dan coba selesaikan soal-soalnya!
Table of Contents
Apa Itu Permutasi?

Permutasi adalah cara menyusun elemen dari suatu himpunan dalam urutan tertentu. Karena urutan diperhatikan, permutasi berbeda dari kombinasi, di mana urutan tidak diperhitungkan.
Berikut ini adalah beberapa jenis permutasi yang umum digunakan.
Permutasi dengan Pengulangan
Pada jenis ini, elemen bisa digunakan lebih dari sekali dalam satu susunan. Rumusnya adalah:
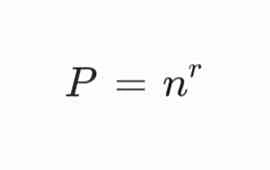
di mana:
- n adalah jumlah total elemen yang tersedia.
- r adalah jumlah elemen yang dipilih dalam satu susunan.
Contohnya:
Misalkan kita ingin membuat kode sandi dengan 4 angka dari 0-9, di mana angka bisa diulang. Maka:
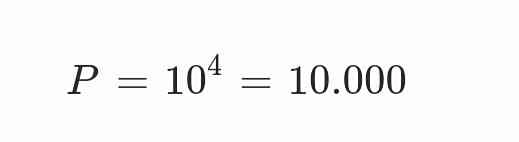
Artinya, ada 10.000 kemungkinan kombinasi angka yang bisa dibuat.
Baca juga: 10 Contoh Soal Energi Kinetik Lengkap Pembahasannya, Mudah hingga Sulit
Permutasi Tanpa Pengulangan
Pada jenis ini, setiap elemen hanya bisa digunakan sekali dalam satu susunan. Rumusnya:
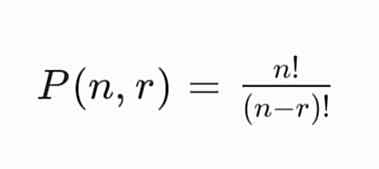
di mana:
- n adalah jumlah total elemen.
- r adalah jumlah elemen yang dipilih.
- ! (faktorial) adalah hasil perkalian semua bilangan bulat positif dari 1 hingga angka tersebut.
Contoh:
Misalkan ada 8 pembalap dalam sebuah balapan, dan kita ingin menentukan siapa yang akan menempati posisi 1, 2, dan 3. Maka:
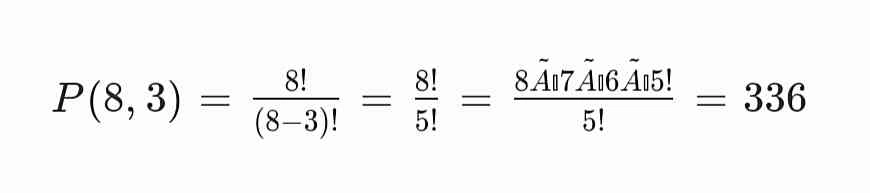
Artinya, ada 336 cara berbeda untuk menentukan tiga pemenang pertama.
Perbedaan Permutasi dan Kombinasi
Permutasi dan kombinasi sering membuat bingung karena keduanya sama-sama berkaitan dengan memilih atau menyusun sesuatu. Tapi, cara kerja keduanya berbeda, terutama dalam hal urutan.
Permutasi digunakan saat urutan elemen yang dipilih penting. Artinya, posisi atau susunan berpengaruh pada hasil akhirnya.
Baca juga: 12 Contoh Iqlab dan Cara Melafalkannya dengan Tepat
Kombinasi digunakan saat urutan tidak penting, yang berarti hanya fokus pada siapa atau apa yang dipilih, tanpa peduli posisi atau urutannya.
Agar lebih jelas, berikut beberapa contohnya:
- Permutasi
- Menyusun huruf dalam sebuah kata, seperti kata dalam kata sandi.
- Memilih juara 1, 2, dan 3 dalam lomba.
- Menyusun struktur organisasi. Misalnya, memilih siapa yang menjadi ketua, sekretaris, dan bendahara.
- Kombinasi
- Memilih tim sepak bola dari sekumpulan pemain.
- Menentukan peserta yang lolos seleksi tahap berikutnya.
- Memilih perwakilan sekolah untuk perlombaan.
Rumus Permutasi
Permutasi adalah cara menyusun atau mengatur elemen dalam suatu himpunan dengan memperhatikan urutan. Jika kita memiliki n elemen dan ingin memilih serta menyusunnya sebanyak r elemen, maka rumus permutasi adalah:
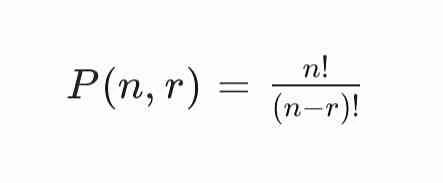
Di mana:
- n! (n faktorial) berarti perkalian berurutan dari n hingga 1, yaitu:
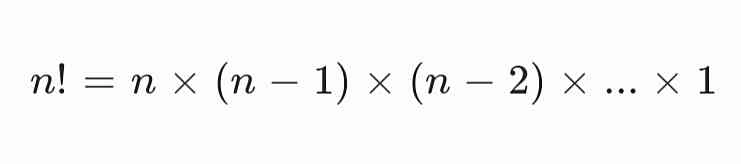
Contoh:
Misalnya, ada 5 peserta dalam lomba, dan kita ingin menentukan siapa yang menjadi juara 1, 2, dan 3. Karena posisi (urutan juara) penting, kita menggunakan permutasi.
Diketahui:
- n = 5 (jumlah peserta)
- r = 3 (jumlah juara yang dipilih)
Jadi, ada 60 cara berbeda untuk menentukan siapa yang menjadi juara 1, 2, dan 3.
Contoh Soal Permutasi dan Pembahasannya
Permutasi adalah konsep matematika yang digunakan untuk menghitung banyaknya cara menyusun atau mengatur suatu kumpulan objek dengan memperhatikan urutan.
Dalam kehidupan sehari-hari, kita sering menemui situasi yang melibatkan permutasi, seperti menyusun kursi di kelas, menentukan pemenang dalam perlombaan, atau membuat kombinasi angka dalam kata sandi.
Agar lebih memahami konsep ini, mari kita lihat beberapa contoh soal permutasi beserta pembahasannya yang akan membantu mengasah pemahaman dan keterampilan dalam menyelesaikan masalah terkait urutan penyusunan.
Contoh Soal Permutasi 1
Berapa banyak cara menyusun ulang huruf dalam kata “MAK” tanpa ada huruf yang hilang atau ditambah?
Pembahasan:
Semua huruf dalam “MAK” berbeda, sehingga jumlah cara menyusunnya adalah:
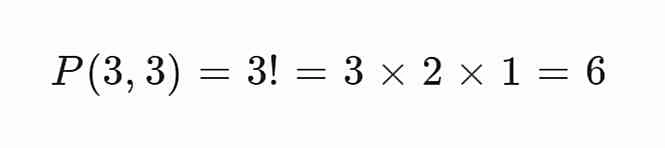
Jadi, ada 6 cara menyusun huruf dalam kata “MAK”.
Contoh Soal Permutasi 2
Dalam sebuah lomba dengan 5 peserta, berapa banyak cara menentukan juara 1 dan juara 2 jika urutan juara diperhatikan?
Pembahasan:
Gunakan rumus permutasi:
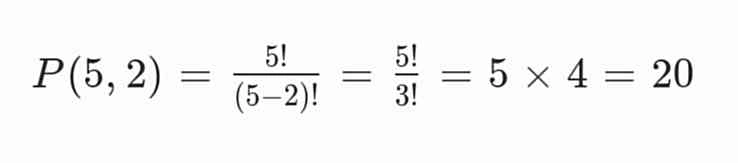
Jadi, ada 20 cara menentukan juara 1 dan 2.
Contoh Soal Permutasi 3
Berapa banyak bilangan tiga digit yang dapat dibentuk dari angka 1, 2, 3, 4, 5 tanpa pengulangan?
Pembahasan:
Karena setiap angka harus unik dan urutannya berpengaruh, gunakan permutasi:
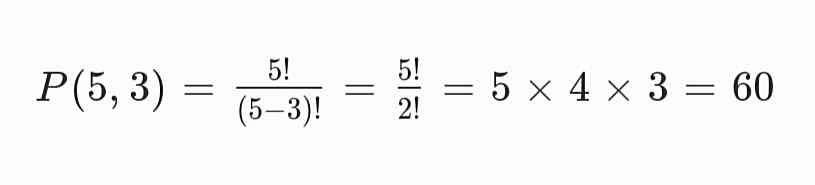
Jadi, ada 60 bilangan tiga digit yang dapat dibentuk.
Contoh Soal Permutasi 4
Ada 6 orang yang akan duduk di 4 kursi berderet. Berapa banyak cara mereka bisa duduk jika setiap kursi hanya diduduki satu orang?
Pembahasan:
Karena posisi duduk berpengaruh, gunakan permutasi:
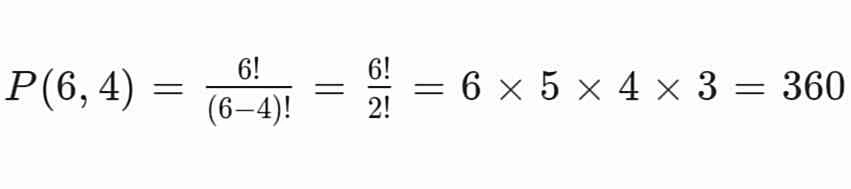
Jadi, ada 360 cara untuk mereka duduk.
Contoh Soal Permutasi 5
Dari 8 pelari, akan dipilih 4 orang untuk berlari dalam estafet, dengan posisi tertentu (pelari pertama, kedua, ketiga, keempat). Berapa banyak susunan tim yang bisa dibuat?
Pembahasan:
Karena urutan pelari berpengaruh, gunakan permutasi:
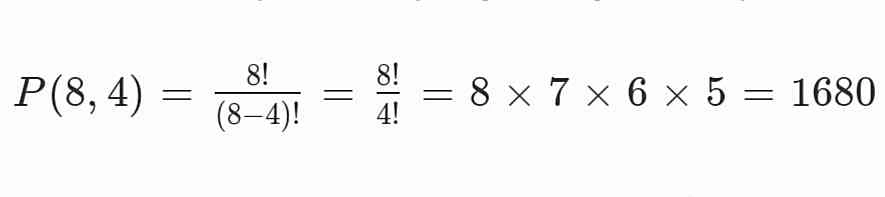
Jadi, ada 1.680 cara menyusun tim estafet.
Contoh Soal Permutasi 6
Sebuah sistem keamanan menggunakan 5 huruf unik yang dipilih dari 9 huruf berbeda. Berapa banyak kode sandi yang bisa dibuat?
Pembahasan:
Karena urutan huruf dalam kode sandi berpengaruh, gunakan permutasi:
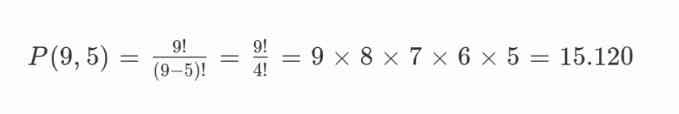
Jadi, ada 15.120 kode sandi yang bisa dibuat.
Contoh Soal Permutasi 7
Ada 10 buku berbeda, tetapi rak hanya bisa menampung 6 buku. Berapa banyak cara menyusun 6 buku tersebut dalam rak jika urutan diperhatikan?
Pembahasan:
Gunakan permutasi karena urutan buku berpengaruh:
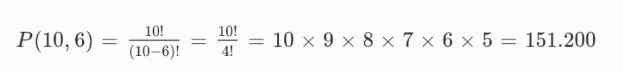
Jadi, ada 151.200 cara menyusun 6 buku di rak.
Contoh Soal Permutasi 8
Berapa banyak cara menyusun ulang huruf dalam kata “RAM” tanpa ada huruf yang hilang atau ditambah?
Pembahasan:
Karena semua huruf berbeda, jumlah cara menyusunnya adalah:
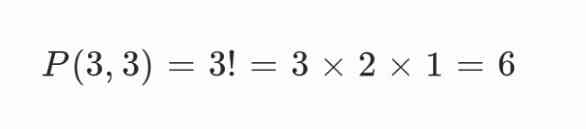
Jadi, ada 6 cara menyusun huruf dalam kata “RAM”.
Contoh Soal Permutasi 9
Dalam suatu tim sepak bola yang terdiri dari 7 pemain, akan dipilih 1 kapten dan 1 wakil kapten. Berapa banyak cara memilih mereka jika urutan jabatan diperhatikan?
Pembahasan:
Gunakan permutasi karena urutan posisi berpengaruh:
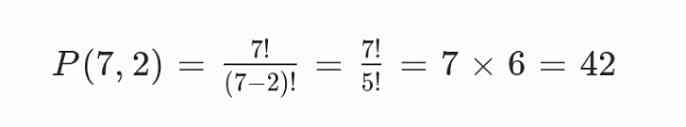
Jadi, ada 42 cara memilih kapten dan wakil kapten.
Contoh Soal Permutasi 10
Berapa banyak cara membuat nomor telepon 5 digit dari angka 0, 1, 2, 3, 4, 5 tanpa ada angka yang berulang?
Pembahasan:
Gunakan permutasi karena urutan angka berpengaruh:
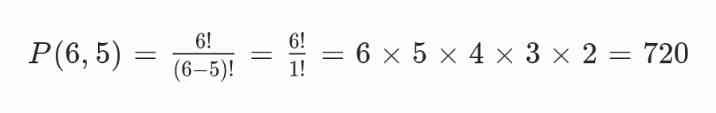
Jadi, ada 720 nomor telepon yang bisa dibuat.
Baca juga: 40 Soal KPK dan FPB Kelas 5 Lengkap dengan Jawaban dan Penjelasannya
Contoh Soal Permutasi 11
Sebuah tim basket memiliki 8 pemain, dan 5 di antaranya akan disusun dalam barisan untuk sesi foto. Berapa banyak cara menyusun mereka jika urutan berpengaruh?
Pembahasan:
Gunakan permutasi karena urutan barisan penting:
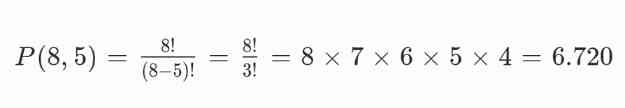
Jadi, ada 6.720 cara menyusun 5 pemain dalam barisan.
Contoh Soal Permutasi 12
Sebuah ruang rapat memiliki 10 kursi, tetapi hanya ada 6 orang yang akan duduk di kursi tersebut. Berapa banyak cara menyusun 6 orang di kursi jika urutan tempat duduk diperhatikan?
Pembahasan:
Gunakan permutasi karena urutan tempat duduk berpengaruh:
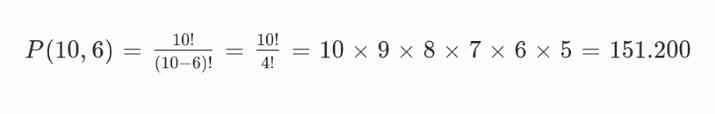
Jadi, ada 151.200 cara menyusun 6 orang di kursi.
Permutasi adalah konsep matematika yang sering kita temui dalam berbagai situasi, mulai dari menyusun kata, menentukan urutan pemenang, hingga mengatur tempat duduk.
Dengan memahami pembahasan soal permutasi, kita bisa lebih mudah menerapkannya dalam kehidupan sehari-hari dan meningkatkan kemampuan berpikir logis.
Jika kamu ingin meningkatkan visibilitas website bisnismu di mesin pencari, Optimaise siap membantu. Sebagai penyedia jasa SEO Malang dan jasa SEO Bali, kami menawarkan strategi optimasi terbaik agar bisnismu muncul di halaman pertama Google.
Jangan biarkan kompetitor mendominasi! Hubungi Optimaise sekarang dan raih lebih banyak pelanggan melalui SEO yang efektif.
