Permutasi bukan sekadar rumus matematika yang bikin pusing kepala. Di balik angka dan simbol, ada logika sederhana yang sebenarnya sering kita temui dalam kehidupan sehari-hari, mulai dari menyusun tempat duduk hingga mengurutkan nama pemenang lomba.
Daripada bingung memikirkan teori, lebih baik langsung saja kita kupas tuntas lewat berbagai contoh soal permutasi lengkap dengan pembahasannya. Siap-siap dibuat paham dan merasa, “Oh, ternyata cuma begini caranya!”
Table of Contents
Apa Itu Permutasi?

Permutasi adalah cara menyusun atau mengatur objek dalam urutan tertentu. Kamu bisa membayangkannya sebagai bagaimana kamu menyusun barang di rak atau mengatur tempat duduk teman-temanmu dalam sebuah foto.
Dalam matematika, permutasi digunakan untuk menghitung berapa banyak cara mengurutkan sejumlah objek tanpa ada yang terulang.
Misalnya, kalau kamu punya tiga buku berjudul A, B, dan C, ada berapa cara menyusunnya di rak? Jawabannya adalah 6 cara, yaitu ABC, ACB, BAC, BCA, CAB, dan CBA. Rumus dasar permutasi adalah n! (n faktorial), yang berarti mengalikan semua bilangan bulat positif dari 1 sampai n. Jadi, untuk 3 buku, hasilnya adalah 3! = 3 × 2 × 1 = 6.
Permutasi penting banget dalam kehidupan sehari-hari, terutama dalam hal yang butuh penyusunan, seperti membuat jadwal, menyusun password, atau mengatur posisi pemain dalam tim. Kalau urutan itu penting, berarti kamu sedang berurusan dengan permutasi.
Perbedaan Permutasi dan Perbandingan

Permutasi dan perbandingan adalah dua konsep penting dalam matematika yang sering kali digunakan untuk menyelesaikan masalah kehidupan sehari-hari.
Permutasi adalah cara untuk menyusun atau mengatur objek dengan memperhatikan urutannya. Jadi, jika kamu memiliki sejumlah objek, setiap susunan yang berbeda dihitung sebagai hasil tersendiri.
Contohnya, misalnya kamu punya tiga benda yang diberi label A, B, dan C. Susunan, seperti ABC, ACB, BAC, BCA, CAB, dan CBA semuanya merupakan permutasi yang berbeda.
Untuk menghitung jumlah permutasi, kamu menggunakan rumus faktorial, yaitu n!, di mana n adalah jumlah objek yang kamu miliki. Rumus ini menghitung perkalian dari semua bilangan bulat dari 1 hingga n.
Sementara itu, perbandingan lebih berfokus pada hubungan antar nilai atau objek dengan menggunakan rasio atau proporsi. Perbandingan tidak memperhatikan urutan, melainkan hanya menekankan seberapa besar satu nilai jika dibandingkan dengan nilai lainnya.
Misalnya, jika kamu memiliki 4 apel dan 6 jeruk, kamu bisa menyatakan perbandingannya sebagai 4:6 atau disederhanakan menjadi 2:3.
Dengan memahami kedua konsep ini, kamu bisa lebih mudah menentukan metode yang tepat untuk menyelesaikan masalah matematika maupun situasi praktis dalam kehidupan sehari-hari.
Pemahaman yang mendalam tentang kedua konsep ini akan membantu kamu tidak hanya dalam pelajaran matematika, tetapi juga dalam membuat keputusan dan menyusun strategi di kehidupan sehari-hari.
Rumus Permutasi

Dari penjelasan sebelumya, permutasi adalah cara menyusun objek dalam urutan tertentu, di mana urutan yang berbeda menghasilkan hasil yang berbeda pula.
Kamu akan menemukan bahwa konsep ini berguna saat menentukan susunan tempat duduk, urutan lomba, atau penjadwalan acara.
Dengan memahami permutasi, kamu bisa menghitung berapa banyak cara untuk menyusun objek yang ada. Setiap perubahan posisi menghasilkan kombinasi baru, sehingga penting untuk tahu bagaimana cara menghitungnya secara tepat.
Ini adalah rumus permutasi:
- Penyusunan semua objek (n!)
- Rumus: n! = n × (n – 1) × (n – 2) × … × 2 × 1
- Contoh: Jika n = 4, maka 4! = 4 × 3 × 2 × 1 = 24.
- Penyusunan sebagian objek (P(n, r))
- Rumus: P(n, r) = n! / (n – r)!
- Contoh: Jika kamu ingin menyusun 3 dari 5 objek, P(5, 3) = 5! / (5 – 3)! = 120 / 2 = 60.
Dengan memahami kedua rumus ini, kamu dapat menyelesaikan berbagai permasalahan yang melibatkan penyusunan objek secara teratur.
Rumus permutasi sangat berguna dalam matematika dan aplikasi nyata, seperti menentukan urutan dalam lomba, penjadwalan, atau pengaturan tempat duduk dalam suatu acara.
Pemahaman mendalam tentang rumus permutasi membantu kamu membuat keputusan dengan perhitungan yang tepat dan akurat. Rumus ini sangat penting.
Waktu Menggunakan Permutasi

Ketika kamu dihadapkan pada situasi di mana urutan objek sangat menentukan hasil akhir, maka kamu perlu menggunakan konsep permutasi.
Permutasi adalah cara untuk menyusun atau mengatur objek secara berurutan sehingga setiap susunan yang berbeda dihitung sebagai satu kemungkinan tersendiri.
Contohnya, jika kamu mengatur posisi pemenang lomba atau menyusun jadwal acara, urutan setiap objek akan berpengaruh terhadap hasil yang kamu dapatkan.
Rumus dasar yang digunakan dalam permutasi ada dua jenis. Pertama, untuk penyusunan seluruh objek, kamu menggunakan rumus n! (n faktorial), yaitu mengalikan semua bilangan dari 1 hingga n. Misalnya, jika n = 4, maka 4! = 4 × 3 × 2 × 1 = 24.
Kedua, jika kamu hanya ingin menyusun sebagian objek dari total n objek, kamu dapat menggunakan rumus P(n, r) = n! / (n – r)!, di mana r adalah jumlah objek yang ingin disusun.
Contohnya, jika kamu ingin menyusun 3 dari 5 objek, maka P(5, 3) = 5! / (5 – 3)! akan memberikan jumlah kemungkinan susunan.
Dengan memahami kapan dan bagaimana menggunakan permutasi, kamu bisa menghitung secara tepat berbagai skenario penyusunan objek. Pemahaman ini tidak hanya berguna dalam konteks akademik, tetapi juga dalam pengambilan keputusan strategis sehari-hari.
Baca juga: 11 Contoh Surat Lamaran Kerja Tulis Tangan Lengkap Tipsnya
Contoh Soal Permutasi
Permutasi merupakan salah satu konsep matematika yang sering muncul dalam berbagai situasi kehidupan sehari-hari. Mulai dari menyusun buku di rak, mengatur tempat duduk, hingga menentukan urutan juara dalam sebuah perlombaan, semuanya melibatkan permutasi.
Meskipun terdengar rumit, sebenarnya konsep ini cukup mudah dipahami jika dilengkapi dengan contoh soal yang tepat.
Pada bagian ini, kita akan membahas berbagai contoh soal permutasi lengkap dengan pembahasannya, sehingga kamu dapat lebih mudah memahami dan menguasai materi ini. Yuk, simak dan pahami setiap langkahnya!
Contoh Soal Permutasi 1
Berapa banyak cara menyusun 4 buku berbeda pada sebuah rak?
Pembahasan:
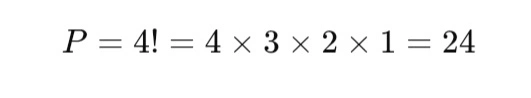
Jadi, ada 24 cara menyusun buku.
Contoh Soal Permutasi 2
Ada 5 orang ingin duduk di 3 kursi yang tersedia. Berapa banyak cara mereka duduk?
Pembahasan:
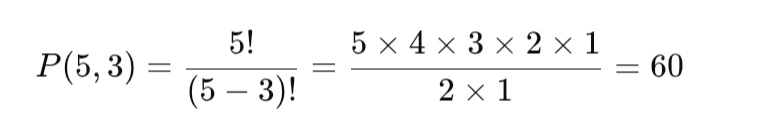
Jadi, ada 60 cara untuk duduk.
Contoh Soal Permutasi 3
Berapa banyak cara menyusun kata “RAMAI” jika semua huruf harus digunakan?
Pembahasan:
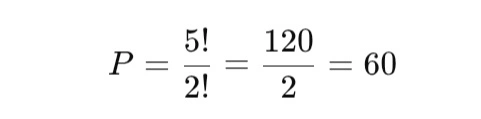
Jadi, ada 60 cara menyusun kata tersebut.
Contoh Soal Permutasi 4
Dari 6 pemain bola, akan dipilih 4 orang untuk posisi berbeda. Berapa banyak susunan yang mungkin?
Pembahasan:
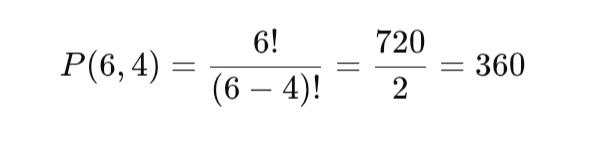
Jadi, ada 360 cara.
Contoh Soal Permutasi 5
Berapa banyak cara menyusun 7 orang dalam sebuah antrean?
Pembahasan:
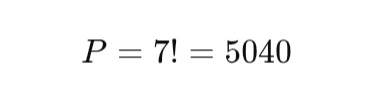
Jadi, ada 5.040 cara.
Contoh Soal Permutasi 6
Ada 8 siswa, dan 3 di antaranya akan dipilih sebagai ketua, wakil ketua, dan sekretaris. Berapa banyak cara memilihnya?
Pembahasan:

Jadi, ada 336 cara.
Contoh Soal Permutasi 7
Berapa banyak cara menyusun 5 huruf dari kata “PELANGI” tanpa huruf yang sama?
Pembahasan:
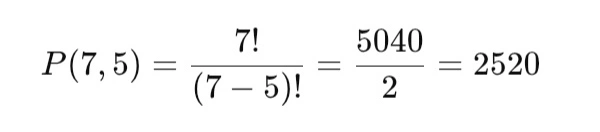
Jadi, ada 2.520 cara.
Baca juga: 3 Cheat Mortal Kombat PS2 untuk Membuka Karakter dan Jurus Rahasia
Contoh Soal Permutasi 8
Dalam sebuah lomba, 10 peserta berlomba untuk 3 posisi juara. Berapa banyak susunan juara yang mungkin?
Pembahasan:
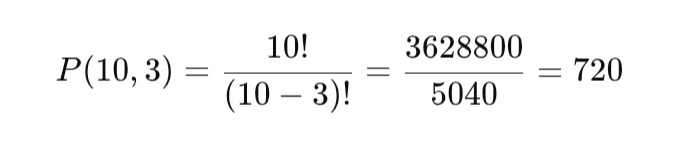
Jadi, ada 720 cara.
Contoh Soal Permutasi 9
Berapa banyak cara menyusun kata “BALON” jika huruf tidak boleh berulang?
Pembahasan:
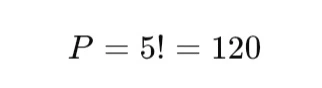
Jadi, ada 120 cara.
Contoh Soal Permutasi 10
Ada 9 peserta yang harus duduk di 5 kursi yang tersedia. Berapa banyak susunan duduknya?
Pembahasan:
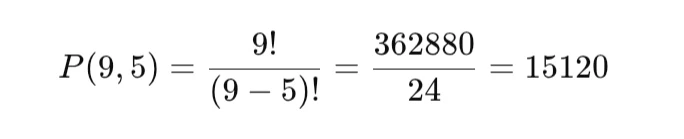
Jadi, ada 15.120 cara.
Permutasi memang bisa terasa rumit di awal, tapi dengan memahami contoh-contoh soal di atas, kamu pasti mulai menangkap polanya.
Kuncinya adalah terus berlatih dan mencoba berbagai variasi soal agar semakin mahir. Jangan biarkan angka membuatmu mundur, justru jadikan tantangan ini sebagai cara melatih logika dan ketelitianmu.
Ngomong-ngomong soal susun menyusun, ini juga berlaku dalam dunia digital. Menyusun strategi SEO yang tepat bisa jadi pembeda antara bisnis yang tenggelam dan bisnis yang tampil di halaman pertama pencarian.
Kalau kamu butuh bantuan profesional untuk mengoptimalkan visibilitas bisnis di Malang atau Bali, Optimaise siap membantu. Kami menawarkan jasa SEO Malang dan jasa SEO Bali dengan pendekatan yang terstruktur dan efektif. Yuk, buat bisnismu semakin terlihat!
