40 Soal KPK dan FPB Kelas 5 Lengkap dengan Jawaban dan Penjelasannya

Saat anak memasuki kelas 5 SD, ia mulai dikenalkan dengan konsep KPK dan FPB yang sangat penting di dalam matematika. Apalagi, materi ini sering muncul dalam berbagai ujian.

Tapi, tahukah kamu bahwa KPK dan FPB sebenarnya bisa membantu kita dalam kehidupan sehari-hari? Mulai dari menghitung waktu bertemunya dua kejadian sampai membagi sesuatu, semua bisa lebih mudah dengan menguasai kedua konsep ini.

Selain belajar di sekolah, anak juga bisa mempelajari konsep ini di rumah untuk memperkuat pemahamannya. Nah, di artikel ini, kamu akan menemukan contoh soal KPK dan FPB kelas 5 SD lengkap dengan jawaban serta penjelasan detailnya. Yuk, langsung saja kita mulai!

Apa Itu KPK dan FPB?

KPK adalah singkatan dari Kelipatan Persekutuan Kecil, yaitu bilangan terkecil yang merupakan kelipatan dari dua atau lebih bilangan. Misalnya, KPK dari 4 dan 5 adalah 20, karena 20 adalah bilangan terkecil yang dapat dibagi oleh 4 dan 5 tanpa sisa.

KPK sering kali digunakan dalam masalah yang melibatkan pengulangan, seperti menentukan waktu atau frekuensi kegiatan yang berulang.

Sementara itu, FPB adalah singkatan dari Faktor Persekutuan Terbesar, yakni bilangan terbesar yang dapat membagi dua atau lebih bilangan tanpa menyisakan sisa.

Baca juga: 5 Cara Buka HP Lupa Kata Sandi Demi Mendapatkan Akses Kembali

Sebagai contoh, FPB dari 12 dan 18 adalah 6, karena 6 adalah faktor terbesar yang membagi kedua bilangan tersebut. Faktor ini sangat membantu dalam menyederhanakan pecahan dan menemukan jumlah yang sama dari kelompok objek.

Perbedaan antara KPK dan FPB

KPK dan FPB adalah dua konsep matematika yang sering digunakan dalam penghitungan terkait bilangan bulat. Meskipun saling berkaitan, keduanya memiliki definisi, tujuan, dan cara penghitungan yang berbeda.

KPK adalah bilangan bulat positif terkecil yang merupakan kelipatan bersama dari dua atau lebih bilangan. KPK digunakan untuk menentukan titik pertemuan kelipatan beberapa bilangan, seperti di dalam kasus pengaturan waktu atau siklus aktivitas yang berulang.

KPK digunakan untuk:

1. Menyelesaikan masalah yang melibatkan siklus berulang.
2. Menyelaraskan beberapa jadwal atau peristiwa.
3. Menghitung waktu pertemuan dari dua kejadian dengan periode berbeda.

Langkah-langkah menghitung KPK:

1. Tentukan kelipatan masing-masing bilangan. Contoh: kelipatan dari 6 adalah {6, 12, 18, 24, …}, dan kelipatan dari 8 adalah {8, 16, 24, 32, …}.
2. Cari kelipatan yang sama dari kedua bilangan.
3. Pilih kelipatan terkecil dari hasil tersebut. Contoh: KPK dari 6 dan 8 adalah 24.

Di sisi lain, FPB adalah bilangan bulat positif terbesar yang dapat membagi habis dua atau lebih bilangan tanpa menyisakan sisa. FPB sering digunakan dalam masalah pembagian, seperti membagi sesuatu menjadi bagian yang sama besar tanpa sisa.

FPB digunakan untuk:

1. Membagi suatu hal menjadi bagian yang sama besar.
2. Menyederhanakan pecahan menjadi bentuk paling sederhana.
3. Menentukan jumlah maksimum kelompok tanpa sisa.

Langkah-langkah menghitung FPB:

1. Tentukan faktor masing-masing bilangan. Contoh: faktor dari 12 adalah {1, 2, 3, 4, 6, 12}, dan faktor dari 15 adalah {1, 3, 5, 15}.
2. Cari faktor yang sama dari kedua bilangan.
3. Pilih faktor terbesar dari hasil tersebut. Contoh: FPB dari 12 dan 15 adalah 3.

Cara Mencari KPK dan FPB dengan Pohon Faktor

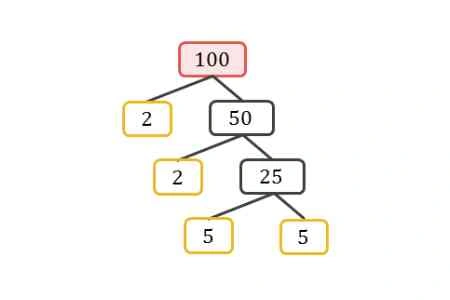
Pohon faktor adalah metode untuk memecah sebuah bilangan menjadi faktor-faktor primanya dengan menggunakan cabang-cabang seperti pohon. Metode ini sangat membantu terutama jika bilangan yang ingin difaktorkan cukup besar, misalnya di atas 50 atau 100.

Cara kerja pohon faktor sebenarnya mirip dengan metode sederhana untuk mencari KPK (Kelipatan Persekutuan Terkecil) dan FPB (Faktor Persekutuan Terbesar), hanya saja lebih terstruktur.

Untuk membuat pohon faktor, pertama-tama tuliskan bilangan yang ingin difaktorkan. Kemudian, buat 2 cabang, salah satu cabang berisi bilangan prima yang menjadi pembagi, sedangkan cabang lainnya berisi hasil pembagiannya. Proses ini dilanjutkan dengan memecah hasil pembagian tersebut hingga semua bilangan di cabang menjadi bilangan prima.

Sebagai contoh, jika kita ingin mencari faktorisasi prima dari 100, langkah-langkahnya adalah:

1. Pecah 100 menjadi 2 × 50
2. Lanjutkan dengan memecah 50 menjadi 2 × 25
3. Terakhir, pecah 25 menjadi 5 × 5

Jadi, faktorisasi prima dari 100 adalah 2 x 2 x 5 x 5 atau 2² x 5².

Misalnya, kita ingin mencari KPK dan FPB dari 36 dan 84. Langkah pertama adalah membuat pohon faktor untuk masing-masing bilangan:

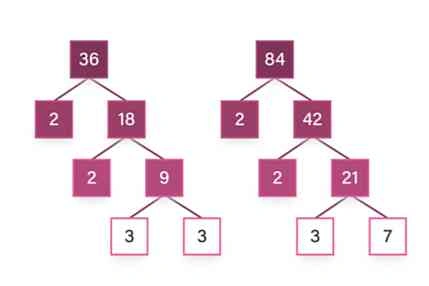
• Faktor prima dari 36 adalah 2 x 2 x 3 x 3 atau 2² x 3²
• Faktor prima dari 84 adalah 2 x 2 x 3 x 7 atau 2² x 3 x 7

Untuk KPK, kita ambil semua faktor prima yang muncul di kedua bilangan, dengan pangkat terbesar untuk setiap faktor. Dari faktor di atas:

• 2 memiliki pangkat tertinggi di kedua bilangan 2²
• 3 memiliki pangkat tertinggi 3²
• 7 hanya muncul di 84

Maka, KPKnya adalah 2² x 3² x 7 = 252.

Untuk FPB, ambil faktor prima yang sama di kedua bilangan, dengan pangkat terkecil:

• 2 memiliki pangkat yang sama di kedua bilangan 2²
• 3 memiliki pangkat terkecil 3¹

Maka, FPBnya adalah 2² x 3 = 12.

Jadi, KPK dari 36 dan 84 adalah 252, dan FPB-nya adalah 12.

Contoh Soal KPK dan FPB Kelas 5 SD Pilihan Ganda dan Cerita

Memahami konsep KPK (Kelipatan Persekutuan Terkecil) dan FPB (Faktor Persekutuan Terbesar) menjadi salah satu keterampilan matematika yang penting bagi siswa kelas 5 SD.

Dengan mempelajari kedua konsep matematika ini, anak-anak dapat melatih kemampuan berpikir logis dan menyelesaikan masalah dalam kehidupan sehari-hari, seperti menentukan waktu kegiatan bersama atau membagi sesuatu dengan adil.

Mari kita pelajari bersama melalui contoh soal KPK dan FPB kelas 5 SD dalam bentuk pilihan ganda dan cerita yang menantang dan menyenangkan berikut ini!

Soal KPK dan FPB Kelas 5 Pilihan Ganda

Tak hanya teori, pemahaman yang mendalam tentang KPK dan FPB dapat membantu anak kelas 5 dalam kehidupan sehari-hari.

Untuk itu, kami telah menyiapkan soal-soal KPK dan FPB kelas 5 dalam bentuk pilihan ganda yang menarik dan penuh variasi, agar kalian bisa menguji pemahaman sekaligus memperkuat kemampuan dalam menemukan KPK dan FPB dengan cara yang mudah dipahami.

Soal KPK dan FPB kelas 5 (1): Berapa KPK dari 8 dan 12?

a) 24

b) 48

c) 16

d) 12

Jawaban: a) 24

Pembahasan:

• Kelipatan 8 adalah 8, 16, 24, 32, dst.
• Kelipatan 12 adalah 12, 24, 36, dst.

Jadi, KPK dari 8 dan 12 adalah 24. Karena 24 adalah kelipatan terkecil yang terdapat dalam kedua deret kelipatan tersebut.

Soal KPK dan FPB kelas 5 (2): Apa FPB dari 15 dan 25?

a) 5

b) 15

c) 25

d) 10

Jawaban: a) 5

Pembahasan:

• Faktor dari 15 adalah 1, 3, 5, dan 15.
• Faktor dari 25 adalah 1, 5, dan 25.

FPB dari 15 dan 25 adalah 5, ini karena 5 menjadi faktor terbesar yang dapat membagi kedua angka tersebut tanpa sisa.

Soal KPK dan FPB kelas 5 (3): Berapa KPK dari 5, 10, dan 15?

a) 30

b) 60

c) 15

d) 45

Jawaban: a) 30

Pembahasan:

• KPK dari 5, 10, dan 15 adalah 30.

30 adalah kelipatan terkecil yang dapat dibagi oleh ketiga angka tersebut tanpa sisa.

Soal KPK dan FPB kelas 5 (4): Apa FPB dari 36 dan 48?

a) 24

b) 18

c) 12

d) 6

Jawaban: c) 12

Pembahasan:

• Faktor dari 36 adalah 1, 2, 3, 4, 6, 9, 12, 18, dan 36.
• Faktor dari 48 adalah 1, 2, 3, 4, 6, 8, 12, 16, 24, dan 48.

Jadi, FPB dari 36 dan 48 adalah 12. 12 adalah faktor terbesar yang dapat membagi kedua angka tersebut tanpa tersisa.

Soal KPK dan FPB kelas 5 (5): Berapa KPK dari 9 dan 14?

a) 63

b) 126

c) 72

d) 42

Jawaban: b) 126

Pembahasan:

• Kelipatan 9 adalah 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, dst.
• Kelipatan 14 adalah 14, 28, 42, 56, 70, 84, 98, 112, 126, dst.

Jadi, KPK dari 9 dan 14 adalah 126.

Soal KPK dan FPB kelas 5 (6): Apa FPB dari 20 dan 50?

a) 10

b) 20

c) 25

d) 5

Jawaban: b) 20

Pembahasan:

• Faktor dari 20 adalah 1, 2, 4, 5, 10, dan 20.
• Faktor dari 50 adalah 1, 2, 5, 10, 25, dan 50,

Maka FPB dari 20 dan 50 adalah 20.

Soal KPK dan FPB kelas 5 (7): Berapa KPK dari 6, 8, dan 10?

a) 60

b) 40

c) 30

d) 120

Jawaban: b) 120

Pembahasan:

• KPK dari 6, 8, dan 10 adalah 120

Karena 120 adalah kelipatan terkecil yang dapat dibagi oleh ketiga angka tersebut tanpa sisa.

Soal KPK dan FPB kelas 5 (8): Apa FPB dari 30 dan 45?

a) 15

b) 30

c) 45

d) 5

Jawaban: a) 15

Pembahasan:

• Faktor dari 30 adalah 1, 2, 3, 5, 6, 10, 15, dan 30.
• Faktor dari 45 adalah 1, 3, 5, 9, 15, dan 45.

Jadi, FPB dari 30 dan 45 adalah 15. Karena ia merupakan faktor terbesar yang dapat membagi kedua angka tersebut tanpa sisa.

Soal KPK dan FPB kelas 5 (9): Berapa KPK dari 7 dan 14?

a) 7

b) 21

c) 28

d) 14

Jawaban: d) 14

Pembahasan:

• Kelipatan 7 adalah 7, 14, 21, 28, dst.
• Kelipatan 14 adalah 14, 28, 42, dst.

Jadi, KPK dari 7 dan 14 adalah 14.

Soal KPK dan FPB kelas 5 (10): Apa FPB dari 24 dan 36?

a) 18

b) 24

c) 12

d) 6

Jawaban: c) 12

Pembahasan:

• Faktor dari 24 adalah 1, 2, 3, 4, 6, 8, 12, dan 24.
• Faktor dari 36 adalah 1, 2, 3, 4, 6, 9, 12, 18, dan 36.

Jadi, FPB dari 24 dan 36 adalah 12.

Soal KPK dan FPB kelas 5 (11): Tentukan KPK dari 24, 48, dan 60!

a) 240
b) 260
c) 280
d) 300

Jawaban: c) 240

Pembahasan:

Langkah pertama adalah mencari faktor prima dari masing-masing angka:

1. Faktor prima dari 24
   • Pecah 24 menjadi 3×8, lalu pecah 8 menjadi 2x2x2
   • Jadi, faktor prima 24 adalah 3×2³
2. Faktor prima dari 48
   • Pecah 48 menjadi 3×16, lalu pecah 16 menjadi 2×2×2×2
   • Jadi, faktor prima 48 adalah 3×2⁴
3. Faktor prima dari 60
   • Pecah 60 menjadi 5×12, lalu pecah 12 menjadi 2×2×3
   • Jadi, faktor prima 60 adalah 5x3x2²

Untuk mendapatkan KPK, ambil faktor prima dengan pangkat terbesar:

• Faktor 2: pilih 2⁴
• Faktor 3: Pilih 3¹
• Faktor 5: Pilih 5¹

Kemudian kalikan:

KPK = 2⁴ x 3 x 5 = 16 x 3 x 5 = 240

Soal KPK dan FPB kelas 5 (12): Tentukan Faktor Persekutuan Terbesar (FPB) dari 30 dan 36!
a) 1
b) 2
c) 3
d) 6

Jawaban: d) 6

Pembahasan:

Untuk menentukan FPB, langkah pertama adalah mencari semua faktor dari kedua angka, yaitu:

1. Faktor-faktor dari 30
   • Angka-angka yang bisa membagi 30 tanpa sisa adalah 1, 2, 3, 5, 6, 10, 15, 30
2. Faktor-faktor dari 36
   • Angka-angka yang bisa membagi 36 tanpa sisa adalah 1, 2, 3, 4, 6, 9, 12, 18, 36

Faktor persekutuan 30 dan 36 adalah:

• Angka-angka yang menjadi faktor dari kedua angka adalah 1, 2, 3, 6

Dari faktor-faktor persekutuan di atas, angka yang paling besar adalah 6.

Soal KPK dan FPB kelas 5 (13): Tentukan Faktor Persekutuan Terbesar (FPB) dari 24 dan 32!

a) 4
b) 2
c) 8
d) 1

Jawaban: d) 8

Untuk mencari FPB, langkah pertama adalah menentukan faktor-faktor dari masing-masing angka:

1. Faktor-faktor dari 24
   • Angka-angka yang bisa membagi 24 tanpa sisa adalah 1, 2, 3, 4, 6, 8, 12, 24
2. Faktor-faktor dari 32
   • Angka-angka yang bisa membagi 32 tanpa sisa adalah 1, 2, 4, 8, 16, 32

Faktor persekutuan 24 dan 32 adalah:

• Angka-angka yang menjadi faktor dari kedua angka adalah 1, 2, 4, 8

Dari faktor-faktor persekutuan tersebut, angka yang paling besar adalah 8.

Soal KPK dan FPB kelas 5 (14): Tentukan Kelipatan Persekutuan Terkecil (KPK) dari 28 dan 35!

a) 140
b) 145
c) 148
d) 150

Jawaban: a) 140

Pembahasan:

Langkah pertama dalam mencari KPK adalah menentukan faktor prima dari kedua angka:

1. Faktor prima dari 28
   • Pecah 28 menjadi 7×4
   • Karena 4 bukan bilangan prima, pecah lagi menjadi 2×2
   • Jadi, faktor prima 28 adalah 7 x 2²
2. Faktor prima dari 35
   • Pecah 35 menjadi 5×7
   • Karena 5 dan 7 adalah bilangan prima, maka faktor prima 35 adalah 5×7

Untuk menghitung KPK, ambil setiap faktor prima dengan pangkat terbesar dari kedua angka:

• Faktor 2: ambil 2² dari 28
• Faktor 5: ambil 5¹ dari 35.
• Faktor 7: ambil 7¹ (karena pangkatnya sama pada kedua angka)

Kemudian kalikan semua faktor prima yang sudah dipilih:

KPK = 2² x 5 x 7 = 4 x 5 x 7 = 140

Soal KPK dan FPB kelas 5 (15): Tentukan Faktor Persekutuan Terbesar (FPB) dari 12 dan 21!
a) 1
b) 3
c) 12
d) 21

Jawaban: b) 3

Pembahasan:

Untuk menentukan FPB, kita ikuti langkah berikut:

1. Cari faktor-faktor dari 12
   • Faktor adalah angka-angka yang dapat membagi habis 12 tanpa sisa. Faktor dari 12 adalah 1, 2, 3, 4, 6, 12
2. Cari faktor-faktor dari 21
   • Faktor adalah angka-angka yang dapat membagi habis 21 tanpa sisa. Faktor dari 21 adalah 1, 3, 7, 21

Faktor persekutuan adalah angka-angka yang menjadi faktor dari kedua bilangan. Faktor persekutuan dari 12 dan 21 adalah 1, 3

Dari faktor persekutuan di atas, angka yang paling besar adalah 3.

Soal KPK dan FPB kelas 5 (16): Ani dan Budi berlatih lari dengan jadwal berbeda. Ani berlatih setiap 4 hari sekali, sedangkan Budi setiap 6 hari sekali. Jika mereka berlatih bersama hari ini, setelah berapa hari mereka akan kembali berlatih bersama?

A. 10 hari
B. 12 hari
C. 14 hari
D. 16 hari

Jawaban: B. 12 hari

Pembahasan:

Untuk menemukan waktu Ani dan Budi berlatih bersama lagi, kita mencari Kelipatan Persekutuan Terkecil (KPK) dari 4 dan 6.

• Kelipatan 4: 4, 8, 12, 16, 20, …
• Kelipatan 6: 6, 12, 18, 24, …
• Kelipatan persekutuan terkecil adalah 12.

Jadi, mereka akan kembali berlatih bersama dalam 12 hari.

Soal KPK dan FPB kelas 5 (17): Seorang penjual buah memiliki 18 apel dan 24 jeruk. Ia ingin membagi buah-buah tersebut ke dalam beberapa kantong dengan jumlah yang sama tanpa sisa. Berapa jumlah buah maksimal dalam setiap kantong?

A. 2 buah
B. 3 buah
C. 6 buah
D. 8 buah

Jawaban: C. 6 buah

Pembahasan:

Untuk menemukan jumlah maksimal buah dalam setiap kantong, kita mencari Faktor Persekutuan Terbesar (FPB) dari 18 dan 24.

• Faktor 18: 1, 2, 3, 6, 9, 18
• Faktor 24: 1, 2, 3, 4, 6, 8, 12, 24
• Faktor persekutuan terbesar adalah 6.

Jadi, jumlah maksimal buah dalam setiap kantong adalah 6 buah.

Soal KPK dan FPB kelas 5 (18): Sebuah lampu berkedip setiap 5 detik, sementara lampu lainnya berkedip setiap 8 detik. Jika kedua lampu berkedip bersamaan sekarang, setelah berapa detik kedua lampu akan berkedip bersamaan lagi?

A. 20 detik
B. 30 detik
C. 40 detik
D. 45 detik

Jawaban: C. 40 detik

Pembahasan:

Kita mencari KPK dari 5 dan 8.

• Kelipatan 5: 5, 10, 15, 20, 25, 30, 35, 40, …
• Kelipatan 8: 8, 16, 24, 32, 40, …
• Kelipatan persekutuan terkecil adalah 40.

Jadi, kedua lampu akan berkedip bersamaan lagi setelah 40 detik.

Soal KPK dan FPB kelas 5 (19): Tina dan Rina memiliki pita sepanjang 30 cm dan 45 cm. Mereka ingin memotong pita tersebut menjadi potongan yang sama panjang tanpa sisa. Berapa panjang maksimal potongan pita tersebut?

A. 3 cm
B. 5 cm
C. 10 cm
D. 15 cm

Jawaban: D. 15 cm

Pembahasan:

Untuk menemukan panjang maksimal potongan pita, kita mencari FPB dari 30 dan 45.

• Faktor 30: 1, 2, 3, 5, 6, 10, 15, 30
• Faktor 45: 1, 3, 5, 9, 15, 45
• Faktor persekutuan terbesar adalah 15.

Jadi, panjang maksimal potongan pita adalah 15 cm.

Soal KPK dan FPB kelas 5 (20): Jika KPK dari dua bilangan adalah 60 dan FPB-nya adalah 5, manakah pasangan bilangan berikut yang mungkin merupakan dua bilangan tersebut?

A. 10 dan 30
B. 15 dan 20
C. 10 dan 15
D. 5 dan 60

Jawaban: B. 15 dan 20

Pembahasan:

Dua bilangan memiliki KPK × FPB = Hasil Perkalian Bilangan.

• Diketahui KPK = 60 dan FPB = 5, maka 10 × 15 = 150.

Mari kita uji opsi yang diberikan:

1. 10 dan 30
   • FPB(10,30) = 10, bukan 5
   • KPK(10,30) = 30, bukan 60
2. 15 dan 20
   • FPB(15,20) = 5
   • KPK(15,20) = 60
3. 10 dan 15
   • FPB(10,15) = 5
   • KPK(10,15) = 30, bukan 60
4. 5 dan 60
   • FPB(5,60) = 5
   • KPK(5,60) = 60

Jadi, pasangan bilangan yang benar adalah 15 dan 20.

Soal KPK dan FPB Kelas 5 dalam Bentuk Cerita

Salah satu cara untuk memahami konsep KPK dan FPB dengan lebih mudah adalah melalui soal cerita. Soal-soal cerita tidak hanya mengasah kemampuan hitung, tetapi juga membantu kita berpikir kritis dalam menyelesaikan masalah nyata.

Pelajari lebih dalam kumpulan soal KPK dan FPB kelas 5 dalam bentuk soal cerita berikut ini yuk!

Soal 1: Sarah dan Ani memiliki beberapa paket kue. Sarah memiliki 18 paket, dan Ani memiliki 30 paket. Mereka ingin membagi paket-paket tersebut sehingga setiap orang mendapatkan jumlah paket yang sama tanpa sisa. Berapa banyak paket yang akan didapatkan oleh masing-masing orang?

Jawaban: FPB dari 18 dan 30 adalah 6. Jadi, Sarah dan Ani dapat membagi paket-paket tersebut sehingga setiap orang mendapatkan 6 paket.

Pembahasan:

• Faktor dari 18 adalah 1, 2, 3, 6, 9, dan 18.
• Faktor dari 30 adalah 1, 2, 3, 5, 6, 10, 15, dan 30.

Sehingga FPB dari 18 dan 30 adalah 6.

Soal 2: Pak Budi memiliki 32 buku dan Pak Joko memiliki 48 buku. Mereka ingin membagi buku-buku tersebut ke dalam kelompok yang sama besar. Berapa jumlah maksimum buku dalam setiap kelompok?

Jawaban: FPB dari 32 dan 48 adalah 16, maka Jumlah maksimum buku dalam setiap kelompok adalah 16 buku.

Pembahasan:

• Faktor dari 32 adalah 1, 2, 4, 8, 16, dan 32.
• Faktor dari 48 adalah 1, 2, 3, 4, 6, 8, 12, 16, 24, dan 48.

16 adalah faktor terbesar yang dapat membagi kedua angka tersebut tanpa sisa.

Soal 3: Anna merayakan ulang tahun setiap 12 hari, dan temannya, Budi, merayakan ulang tahun setiap 15 hari. Jika mereka merayakan ulang tahun pada hari yang sama pada 1 Januari, kapan mereka akan merayakan ulang tahun bersama lagi?

Jawaban: pada 1 Maret

Pembahasan:

Untuk mengetahui kapan Anna dan Budi akan merayakan ulang tahun bersama lagi, kita harus mencari KPK dari 12 dan 15.

• Faktorisasi 12 adalah 2² x 3
• Faktorisasi 15 adalah 3 x 5
• KPK dari 12 dan 15 adalah 2² x 3 x 5 = 60

Jadi, Anna dan Budi akan merayakan ulang tahun bersama lagi dalam 60 hari. Jika mereka merayakan ulang tahun pada 1 Januari, mereka akan merayakan ulang tahun bersama lagi pada 1 Maret, 60 hari setelah 1 Januari.

Soal 4: Dua adik memiliki 18 dan 24 balon. Mereka ingin membagi balon-balon tersebut dalam kantong yang sama besar tanpa ada balon yang tersisa. Berapa banyak balon maksimum dalam setiap kantong?

Jawaban: 6 balon

Pembahasan:

• Faktorisasi 18 adalah 2 x 3²
• Faktorisasi 24 adalah 2³ x 3
• FPB dari 18 dan 24 adalah 2 x 3 = 6.

Jadi, jumlah maksimum balon dalam setiap kantong adalah 6 balon.

Soal 5: Mia dan Sita memiliki dua jenis kegiatan yang diadakan setiap 8 hari dan 12 hari. Jika keduanya memulai kegiatan pada 1 Februari, kapan mereka akan melakukan kegiatan tersebut pada hari yang sama lagi?

Jawaban: 25 Februari

Pembahasan:

• Faktorisasi 8 adalah 2³
• Faktorisasi 12 adalah 2² x 3
• KPK dari 8 dan 12 adalah 2³ x 3 = 24

Jadi, Mia dan Sita akan melakukan kegiatan pada hari yang sama lagi dalam 24 hari. Jika mereka mulai pada 1 Februari, maka mereka akan melakukan kegiatan bersama lagi pada 25 Februari, 24 hari setelah 1 Februari.

Soal 6: Joko dan Lina memiliki 24 dan 36 pensil. Mereka ingin membagi pensil-pensil tersebut dalam jumlah yang sama per kotak. Berapa jumlah maksimum pensil per kotak?

Jawaban: 12 pensil

Pembahasan:

• Faktor dari 24 adalah 1, 2, 3, 4, 6, 8, 12, 24.
• Faktor dari 36 adalah 1, 2, 3, 4, 6, 9, 12, 18, 36.

Jadi, FPB dari 24 dan 36 adalah 12.

Baca juga: 10 Contoh Soal Mikrometer Sekrup Lengkap dengan Jawaban dan Pembahasannya

Soal 7: Fani dan Titi memiliki 48 dan 60 kue. Mereka ingin mengemas kue dalam kotak dengan ukuran yang sama tanpa ada kue yang tersisa. Berapa ukuran maksimum kotak yang dapat digunakan?

Jawaban: 12 kotak

Pembahasan:

• Faktor dari 48 adalah 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
• Faktor dari 60 adalah 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
• FPB dari 48 dan 60 adalah 12.

Jadi, ukuran maksimum kotak yang dapat digunakan adalah 12 kue.

Soal 8: Tina memiliki 90 kue dan Sari memiliki 120 kue. Mereka ingin membagi kue tersebut ke dalam paket yang sama besar. Berapa jumlah maksimum kue di dalam setiap paket?

Jawaban: 30 kue

Pembahasan:

• Faktor dari 90 adalah 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90.
• Faktor dari 120 adalah 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120.
• FPB dari 90 dan 120 adalah 30.

Jadi, setiap paket bisa berisi 30 kue.

Soal 9: Dua acara tahunan diadakan setiap 15 hari dan 20 hari. Jika acara pertama diadakan pada 1 Januari, kapan kedua acara tersebut akan diadakan pada hari yang sama lagi?

Jawaban: 1 Maret

Pembahasan:

• Faktorisasi 15 adalah 3 x 5
• Faktorisasi 20 adalah 2² x 5
• KPK dari 15 dan 20 adalah 2² x 3 x 5 = 60

Jadi, kedua acara tersebut akan diadakan pada hari yang sama lagi dalam 60 hari.

Jika acara pertama diadakan pada 1 Januari, maka kedua acara tersebut akan diadakan pada 1 Maret. Karena 60 hari setelah 1 Januari adalah 1 Maret.

Soal 10: Anna membuat kue setiap 8 sendok makan dan 12 sendok makan. Jika dia menggunakan sendok makan untuk takaran bahan yang sama setiap kali, maka berapa takaran maksimum yang dapat dia gunakan agar takaran sama setiap kali?

Jawaban: 24 sendok makan

Pembahasan:

• Faktorisasi 8 adalah 2³
• Faktorisasi 12 adalah 2² x 3
• KPK dari 8 dan 12 adalah 2³ x 3 = 24

Jadi, takaran maksimum yang dapat dia gunakan adalah 24 sendok makan.

Soal 11: Doni memiliki 24 pensil dan 36 penghapus. Ia ingin membagikan pensil dan penghapus tersebut ke beberapa kelompok dengan jumlah yang sama tanpa ada sisa. Berapa jumlah kelompok maksimum yang bisa dibuat?

Jawaban: 12 kelompok

Pembahasan:

• Faktorisasi prima:
  • 24 = 2³ x 3
  • 36 = 2² x 3²
• Ambil faktor yang sama dengan pangkat terkecil:
  • FPB = 2² x 3 = 12

Soal 12: Sebuah lampu merah di persimpangan A menyala setiap 12 detik, sedangkan di persimpangan B menyala setiap 18 detik. Jika kedua lampu menyala bersamaan pada pukul 07:00, kapan kedua lampu akan menyala bersamaan lagi?

Jawaban: pada pukul 07:00:36.

Pembahasan:

• Faktorisasi prima:
  • 12 = 2² x 3
  • 18 = 2 x 3²
• Ambil semua faktor dengan pangkat terbesar:
  • KPK = 2² x 3² = 36
• Jadi, kedua lampu akan menyala bersamaan lagi setelah 36 detik. Pada pukul 07:00:36.

Soal 13: Ibu memiliki dua jenis pita dengan panjang masing-masing 48 cm dan 72 cm. Ia ingin memotong kedua pita tersebut menjadi potongan-potongan yang sama panjang tanpa ada sisa.

1. Berapa panjang potongan pita maksimum yang dapat dibuat?
2. Jika ibu ingin menyambungkan kedua pita menjadi satu pita panjang, berapa panjang pita terpendek yang bisa dibuat?

Jawaban:

1. Panjang potongan pita maksimum adalah 24 cm.
2. Panjang potongan pita terpendek adalah 144 cm.

Pembahasan:

1. Mencari FPB:
   • Faktorisasi prima:
     • 48 = 2⁴ x 3
     • 78 = 2³ x 3²
   • Ambil faktor yang sama dengan pangkat terkecil:
     • FPB = 2³ x 3 = 24
   • Jadi, panjang potongan pita maksimum adalah 24 cm.
2. Mencari KPK:
   • Ambil faktor yang sama dengan pangkat terbesar:
     • KPK = 2⁴ x 3² = 144
   • Jadi, panjang potongan pita terpendeknya adalah 144 cm.

Soal 14: Dina memukul gong setiap 20 menit, sedangkan Fina memukul gong setiap 15 menit. Jika mereka memukul gong bersama-sama pada pukul 08:00, pada pukul berapa mereka akan memukul gong bersama-sama lagi?

Jawaban: pada pukil 09:00

Pembahasan:

• Faktorisasi prima:
  • 20 = 2² x 5
  • 15 = 3 x 5
• Ambil faktor yang sama dengan pangkat terbesar:
  • KPK = 2² x 3 x 5 = 60
• Jadi, mereka akan memukul gong bersama-sama lagi setelah 60 menit atau 1 jam. Pada pukul 09:00.

Soal 15: Pak Budi memiliki 30 apel dan 45 jeruk. Ia ingin membagikan buah-buahan tersebut ke beberapa kantong plastik dengan jumlah yang sama. Berapa jumlah apel dan jeruk yang ada di setiap kantong plastik jika jumlah kantong plastik maksimum?

Jawaban: setiap kantong berisikan 2 apel dan 3 jeruk

Pembahasan:

• Faktorisasi prima:
  • 30 = 2 x 3 x 5
  • 45 = 3² x 5
• Ambil faktor yang sama dengan pangkat terkecil:
  • FPB = 3 x 5 = 15
• Jadi, setiap kantong plastik akan berisi:
  • 30/15 = 2 apel
  • 45/15 = 3 jeruk

Soal 16: Dina dan Rina memiliki jadwal olahraga berbeda. Dina berlari setiap 3 hari sekali, sedangkan Rina bersepeda setiap 5 hari sekali. Jika hari ini mereka berolahraga bersama, setelah berapa hari mereka akan bertemu lagi dalam olahraga bersama?

Jawaban: 15 hari

Untuk mencari kapan mereka akan bertemu lagi, kita cari Kelipatan Persekutuan Terkecil (KPK) dari 3 dan 5.

• Kelipatan 3: 3, 6, 9, 12, 15, 18, …
• Kelipatan 5: 5, 10, 15, 20, 25, …
• Kelipatan persekutuan terkecil adalah 15.

Jadi, Dina dan Rina akan berolahraga bersama lagi dalam 15 hari.

Soal 17: Seorang ibu memiliki 28 kue cokelat dan 42 kue keju. Ia ingin membagikan kue-kue tersebut ke dalam beberapa kotak dengan jumlah yang sama tanpa sisa. Berapa jumlah kotak terbanyak yang bisa dibuat?

Jawaban: 14 kotak

Pembahasan:

Untuk menentukan jumlah kotak terbanyak, kita cari Faktor Persekutuan Terbesar (FPB) dari 28 dan 42.

1. Faktor 28: 1, 2, 4, 7, 14, 28
2. Faktor 42: 1, 2, 3, 6, 7, 14, 21, 42
3. Faktor persekutuan terbesar adalah 14.

Jadi, jumlah kotak terbanyak yang bisa dibuat adalah 14 kotak, dengan masing-masing kotak berisi 2 kue cokelat dan 3 kue keju.

Soal 18: Di sebuah ruangan, ada dua lampu yang berkedip dengan interval berbeda. Lampu pertama berkedip setiap 9 detik sekali, dan lampu kedua berkedip setiap 12 detik sekali. Jika kedua lampu berkedip bersamaan sekarang, setelah berapa detik keduanya akan berkedip bersamaan lagi?

Jawaban: 36 detik

Pembahasan:

Kita cari KPK dari 9 dan 12.

• Kelipatan 9: 9, 18, 27, 36, 45, …
• Kelipatan 12: 12, 24, 36, 48, …
• Kelipatan persekutuan terkecil adalah 36.

Jadi, kedua lampu akan berkedip bersamaan lagi setelah 36 detik.

Soal 19: Seorang guru memiliki 48 cm pita merah dan 64 cm pita biru. Ia ingin memotong pita-pita tersebut menjadi potongan yang sama panjang tanpa sisa. Berapa panjang maksimal setiap potongan pita?

Jawaban: 16 cm

Pembahasan:

Untuk menemukan panjang maksimal potongan pita, kita cari FPB dari 48 dan 64.

1. Faktor 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
2. Faktor 64: 1, 2, 4, 8, 16, 32, 64
3. Faktor persekutuan terbesar adalah 16.

Jadi, panjang maksimal setiap potongan pita adalah 16 cm.

Soal 20: Seorang petani memiliki 40 apel dan 50 jeruk. Ia ingin mengemas buah-buah tersebut ke dalam kantong dengan jumlah yang sama di setiap kantong.

Jika kantong yang dibuat hanya 5, berapa jumlah apel dan jeruk dalam setiap kantong?

Jawaban: 5 kantong, 8 apel & 10 jeruk

Pembahasan:

1. Mencari FPB dari 40 dan 50 untuk jumlah kantong maksimal:
   • Faktor 40: 1, 2, 4, 5, 8, 10, 20, 40
   • Faktor 50: 1, 2, 5, 10, 25, 50
   • FPB-nya adalah 10, sehingga kantong maksimal yang bisa dibuat adalah 10 kantong dengan masing-masing kantong berisi 4 apel dan 5 jeruk.
2. Jika hanya dibuat 5 kantong, maka total buah dibagi 5:
   • 40 apel ÷ 5 = 8 apel per kantong
   • 50 jeruk ÷ 5 = 10 jeruk per kantong

Jadi, jika hanya dibuat 5 kantong, setiap kantong berisi 8 apel dan 10 jeruk.

Mempelajari soal-soal KPK dan FPB kelas 5 ini sangatlah penting untuk memperkuat kemampuan matematika dasar anak. Dengan latihan soal-soal KPK dan FPB kelas 5 yang konsisten, anak akan lebih siap menghadapi berbagai ujian serta mengasah kemampuan logika dalam menyelesaikan masalah sehari-hari.

Selain penting dalam dunia pendidikan, keterampilan menguasai hal-hal teknis seperti matematika, juga bisa diterapkan dalam dunia digital. Salah satunya di dalam SEO (Search Engine Optimization).

Jika kamu tertarik untuk mengimplementasikan strategi SEO untuk bisnismu, kamu bisa menggunakan jasa SEO dari Optimaise yang dapat disesuaikan dengan tujuan bisnismu.

Sebagai digital marketing agency Malang, Optimaise juga menawarkan jasa press release Dan jasa penulisan artikel SEO-friendly untuk membantu website-mu tampil lebih optimal di mesin pencari. Jadi, tunggu apa lagi? Kunjungi Optimaise sekarang dan mulai tingkatkan kualitas situs webmu secara menyeluruh!